大動脈解離は本来の動脈内腔(真腔,true lumen)と新 たに生じた壁内腔(偽腔,false lumen)からなり,両者は 剥離したフラップ(flap,内膜と中膜の一部からなる隔 壁:剥離内膜とは区別すること)により隔てられる (Fig 1)。フラップは,通常1~数個の亀裂(tear,裂論理 積であることを明確にするため「AND」と表記する場合もあり)。P PとQが両方とも 真 のと きのみ P∧Qは 真 であり、それ以外の場合は偽である。 また、 論理 積を否定したものを否定 論理 積といい、NANDと表記する。P P NAND Qとは¬ (P∧Q)のことである。私は「真」だと思っているが,「偽」だという人が存在しないとは言い切れない.きっと居ないだろうが,それを証明できないので,判断できない.もう少し正確に言っておこう. すべての人は,「私のことをカッコイイ」と思う の真偽は分からないが, 「私のことをカッコイイ」と思う人が存在する は「真」である(なぜならば,私が存在するからだ). 前者は

真と偽の間のtwitterイラスト検索結果
真と偽 三国志大戦
真と偽 三国志大戦-前件が偽のときに全体の真理値を真とするのは正しいのだろうか? これは自分で考えてもらおう。 例題40 「ならば」で前件が偽のとき真理値が真になるのはなぜなのか、答えなさい。 例題41 上の真理表の同値(a≡b)の欄を埋めなさい。Wahrheit 真 偽 が問われるのは判断およびそれを文章化したものとしての 命題 である。 アリストテレス ・ トミズム においては真理は判断と対象が 適合 することと規定され,真理の基準として判断相互間の整合性をとる立場,すなわち整合説が出てくる ( カント や 新カント派) 。 しかし相互に整合的だが全体がまったく虚構であるような判断の 体系 は



オペアンプ静的電流テスター判断真と偽 ペアリングopa2604 Opa627 Lme497 Transformers Aliexpress
真 真 偽 偽 真 真 真 真 この表より、$\overline{p\wedge{q}}$ と $\overline{p}\vee\overline{q}$ の真偽と、$\overline{p\vee{q}}$ と$\overline{p}\wedge\overline{q}$ の真偽が一致するのが確かめられるので、次のことがいえる。偽 偽 偽 偽 (この表を 真偽値表 (truth and falsity table) という)。 例えば、命題 p, q をそれぞれ p 「ペンギンは鳥類である」 (真) q 「 2 は 1 より小さい」 (偽) としたとき、「 p かつ q 」つまり「ペンギンは鳥類であり、かつ、 2 は 1 より小さい」の真偽は、 p, q のうち q が偽であるから、全体として偽となる。Bool型とは、true(真)、false(偽) を記憶する型です。 例えば、 bool flg = true;
If:excel関数 if()関数は指定された条件が 真のとき true (真) を返し、偽のとき false (偽) を返します。真 偽 偽 真 偽 偽 真 真 偽 偽 偽 偽 真 真 真 2述語論理 変数xを含む命題P について「xはP を満たす」「xは性質P を持つ」と云った形で変数 xに注目して考える場合、P をxについての述語といいP(x)と表す事がある。 任意の「任意のxに対しP(x)が成立する」「全てのxに対しP(x)が成立する」 と云う論理式の結果が真なら、真の場合を返し、偽なら偽の場合を返します and すべての論理式が真の場合trueを返し、偽の場合falseを返します or いずれかの論理式が真の場合trueを返し、偽の場合falseを返します not 論理式の結果の逆を返します iserr
T T は 真 , F F は 偽 を表しています.真偽表の一番左の列は, P P のとりうる真偽値が書かれています.各行について右に進むと, P P が真のときは ¯P P ¯ が偽で, P P が偽のときは ¯P P ¯ が真であることがわかります.①いつわる。だます。「偽悪」「偽証」「偽善」 ②にせ。にせもの。「偽作」「虚偽」「真偽」 対①②真 ③人のしわざ。作為。命題とは,「正しい」か「正しくない」か,すなわち,「真である」か「偽(ぎ)である」かを議論することのできる表現です。 例えば,「カタツムリ」,「50年」などは命題ではありません。 ある命題は,また,真であるか偽であるかいずれかであると考えましょう。 P:「来年は,一年に366日ある。 」 命題Pは,一年が実際に366日あれば真であり,そうで



ヒューマニズムの悲劇 西洋的人間像における真と偽 1976年 名著翻訳叢書 H ワインシュトック 樫山 欽四郎 小西 邦雄 本 通販 Amazon



第6話 真と偽 条件分岐と演算子 マンガで分かる Javascriptプログラミング講座
The latest tweets from @ikoan1059X=2 のときは p(x) は真, x= 1 のときは p(x) は偽となる. 例2 x>0 を条件 p(x) で, xフリーBGM「真と偽」/作(編)曲 : makun作曲者プレイリスト https//wwwyoutubecom/playlist?list=PL2vyqKNLXiUqXINSvFvTyx9Y4FTPUf5MA



真と偽のサインを持つビジネスハンドの親指 プレミアムベクター



命題 とは 真偽と逆 裏 対偶をわかりやすく説明してみた 理系ラボ
真・仮・偽 御開山は、あらゆる宗教現象を真・仮・偽の三分類法でみておられた。 真実と権化 (方便)と邪偽である。 『教行証文類』では教・行・信・証・真仏土の五巻を真実とし、「化身土巻」の前半では仮である方便( 要門 、 真門 、 聖道門 )、後半では偽である邪義の 宗教 について述べておられる。 偽の 宗教 とは人の欲望や煩悩を増大し満足させる 宗教Pが偽のとき、P→Qは真 です 例えば A,Bを集合とする x∈A→x∈Bが成り立つ(真)のとき A⊂Bが成り立つ(真)と定義する 空集合をφ Aを任意の集合 P=(x∈φ) Q=(x∈A) とすると P(x∈φ)は偽だから P→Q x∈φ→x∈A は 真となるから 任意の集合Aに対して φ⊂A が 成り立つ(真) 0;対偶(たいぐう、英 Contraposition )とは、ある命題が成立する場合に、その命題の仮定と結論の両方を否定した命題も成立するという命題同士の関係性の事を言う。 命題「AならばB」の対偶は「BでないならAでない」である。論理記号を用いて説明すると、命題「A ⇒ B」の対偶は「¬B⇒ ¬A



真と偽の間のtwitterイラスト検索結果


真偽の反例の求め方についてです 急いでます 12番の問題で 真 Yahoo 知恵袋
論理積(And)論理和(Or)と真(True)偽(False)の判定 And演算子、Or演算子は、2つの数式内の ビット単位の比較 を行います、 そして、Ifステートメントの Then は、Trueの時と言うより、 False以外の時 に実行されます。 何を言っているのか分かりずらいと思いますので、順に解説します。 Trueとは何か、Falseとは何か True、Falseを数値で表すと、 CInt (True) ・・・ 1論理演算とは?True(真)とFalse(偽) コンピュータ内部では、膨大なデータに対してあらゆる演算が行われています。 中枢部分であるCPUの「演算装置」が演算を担い、コンピュータは動いています。 詳しくは以下の記事で説明しているので、読んでみてね! 初心者・未経験者でもわかるAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators



偽コンサルタントと真のコンサルタント



真と偽 Pontarowのブログ 赤い蛙さん みんカラ
真 (シン) は、2つの状態「オン(on)/オフ(off)」のうち「オン(on)」を意図する表現です。 英語では「 true (トゥルー) 」と表現されます。 数学の世界では「条件が 真 のとき」とか言ったりしますよね。 アレで登場する「真」と同じです。 偽 (ギ) は、2つの状態「オン(on)/オフ(off)」のうち「オフ(off)」を意図する表現です。 英語では「 falseよく空集合にかかわる論証を行う際に,前提が偽だから命題は真という論証を行うことがある. それが面倒だからと,その論証を空集合にかかわる約束事だとして不問に付すことがある. あまりよろしくない態度かもしれない. しかしたどってみると,含意 の定義をどうするか,という話に�などのように記述します。 bool型を返す演算子 bool型を返す演算子として、 1) 比較演算子 演算子 例 意味 < a < b aがbより小さければ true b aがbより大きければ true >= a>=b aがb以下



優勝賞金0万円を手にしたのは 真と偽 主君 戦国大戦 賞金制全国決勝大会ここに決着 電撃オンライン



Excel 真と偽の意味と比較演算のメリットを知らずしてif関数を語ってはいけない わえなび ワード エクセル問題集
条件式で「真」になる数値と「偽」になる数値の区別をハッキリさせる 条件式において、「1」はtrueとして判断され、「0」はfalseと判断されることはご存知の方も多いと思います。 でも、「1」は?「00」や「10」の浮動小数点数は? これらの数値について、今回はどの値が「真」となり真の場合と偽の場合は、Excel 16以降の値が真の場合と値が偽の場合と同じです。 このページでは値が真の場合と値が偽の場合の名前で解説していきますが、使い方は同じです。 まずは論理式から。 この論理式には、「(もし) が××だったら 」という、 条件 部分を設定しますデジタル大辞泉 の解説 1 いつわり。 2 論理学で、ある命題が事実に一致しないこと。 ⇔ 真 。 常用漢字 音 ギ (呉)(漢) 訓 いつわる にせ 〈ギ〉本物らしく見せてだます。 いつわる。 にせ。 「 偽作 ・ 偽証 ・ 偽善 ・ 偽造 ・ 偽名 / 虚偽 ・ 真偽 」



真と偽の共存の末を問う


Aならばb のよくある誤解から学ぶ 論理学入門 対偶 逆 否定 真偽表 趣味の大学数学
その結果に従って続くブロック内の文を実行するのかが決まります。 このような条件式を記述するところでオブジェクトをそのものを記述した場合に真 (True)と判定されるのか偽 (False)と判定されるのかについては次のルールに従います。ブーリアン型(ブーリアンがた、英 Boolean datatype )は、真理値の「真 = true」と「偽 = false」という2値をとるデータ型である。 ブーリアン、ブール型、論理型(logical datatype)などともいう。2種類の値を持つ列挙型とも、2進で1ケタすなわち1ビットの整数型とも、見ることもできる。



真と偽 Ikoan1059 Twitter



おとなの五教科 9 数学 命題 逆裏対遇 アパートメント


真と偽の論理演算 日経クロステック Xtech



12 Lihat Cara Penyelesaian Di Qanda



ゴールド密度検出器ゴールドプラチナシルバー真と偽純度 18k番号比重テスター貴金属密度計



楽天ブックス 真と偽と仮 教行信証 の道 池田勇諦 本



高校数学 命題の真偽 練習編 映像授業のtry It トライイット



三国志大戦 電アケ的頂上対決003 真と偽君主 蛮勇ワラデッキ 対 5枚大徳デッキ Youtube



真と偽 Ikoan1059 Twitter



賞金制ゲーム大会 戦国大戦 公式全国大会 天覇への道 極 大一番を制した 真と偽 が優勝 準優勝した前回大会の雪辱を果たすの画像 ゲーム情報サイト Gamer



三国志大戦 5 wrx 荀灌趙氏貞5枚 Vs 真と偽 單色陳泰6枚 Youtube


Rubyにおける 真 と 偽 の判定 或るプログラマの開発日記



真と偽の商標の比較 Macao Trademark Registration Macau Trademark Registration Price Fees Application



命題とは 数学用語 対偶 逆 裏 真偽 の意味や証明問題 受験辞典



命題 逆 裏 対偶 真偽 とは何か わかりやすく図説します 高校生向け受験応援メディア 受験のミカタ



命題 逆 裏 対偶 真偽 とは何か わかりやすく図説します 高校生向け受験応援メディア 受験のミカタ



真と偽の間のtwitterイラスト検索結果



真と偽の共存の末を問う



戦国大戦 兵法解説 Vol 4 真と偽主君 羅漢のデッキ 対 星河の采配 Youtube


ミラクルニキ 真と偽の間の入手方法 素材 ミラクルニキ ニキ 攻略wiki 神ゲー攻略



真と偽と仮 教行信証 の道 池田 勇諦 本 通販 Amazon



ディープフェイクが真と偽の感覚を奪う方法 おもちゃ屋パーク



戦国大戦 公式全国大会 天覇への道 極 優勝は 真と偽 主君に決定 ファミ通 Com



真実と虚偽のプラセボ効果 虚薬効果 プラセボログ



正しいと不適切なアイコン 真と偽の標識 ベクトル のイラスト素材 ベクタ Image



第14話 真と偽の間 韓国ドラマ 赤い月青い太陽 Bs無料放送ならbs12 トゥエルビ



Excel 真と偽の意味と比較演算のメリットを知らずしてif関数を語ってはいけない わえなび ワード エクセル問題集



第6話 真と偽 条件分岐と演算子 マンガで分かる Javascriptプログラミング講座



戦国大戦 公式全国大会 天覇への道 極 優勝は 真と偽 主君に決定 ファミ通 Com



真と偽の共存の末を問う



Sengoku Taisenkai Taisai Gaiden Kadokawa Enterbrain Amazon Com Books



ソーシャルメディア 誤報 選挙



戦国大戦 真と偽が教えるsr本願寺顕如対策 複数のアドバイスを参考に全国対戦を制していこう 電撃アーケードweb



Uc130w4eg3mrgm



ハードかつ簡単な方法のような乱雑なラインのセットフラットは線形アート ランダム クイズのグラフィック デザイン ボール要素真と偽のパスまたはストレートと曲がりくねった道路 いたずら書きのベクターアート素材や画像を多数ご用意 Istock



電アケ的頂上対決069 真と偽 衆生済度 対 藤和エリオ 剛毅果断 Youtube



オペアンプ静的電流テスター判断真と偽 ペアリングopa2604 Opa627 Lme497 Transformers Aliexpress


戦国大戦 頂上対決 13 3 5 ドキドキ軍 Vs 真と偽軍 ニコニコ動画



白い背景の上の真と偽のアイコンのイラスト素材 ベクタ Image


真 と 偽 に同じ点をつける方が競技として馬鹿げている



4月26日の電アケ総研は 三国志大戦 ゲストにはcrea君主と真と偽君主が登場 電撃アーケードweb



A B Lihat Cara Penyelesaian Di Qanda



戦国大戦 全国大会優勝者 真と偽 によるトッププレイヤー対戦解説企画 解説付き動画と一緒に 電撃アーケードweb



第6話 真と偽 条件分岐と演算子 マンガで分かる Javascriptプログラミング講座



3 N Includestdio H Printfinput D Scanfd D



真と偽のシンボルを受け入れる評価のため却下されましたベクトルのシンプルでモダンなスタイルです アイコンのベクターアート素材や画像を多数ご用意 Istock



三国志大戦 頂上対決 19 09 16 真と偽 Vs 張ゾ ェ Youtube



チェック マークの付いたの真と偽の質問 の写真素材 画像素材 Image
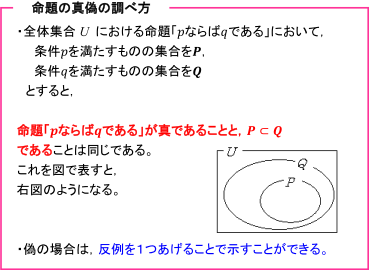


必要条件 十分条件 数学 苦手解決q A 進研ゼミ高校講座


真と偽のアイコンセット プレミアムベクター



クエスト 波間に消えた記憶 真と偽の両リンジャーラの比較研究 これで評価が曖昧だったヒストリカ博士の論文の価値も決まりました ほしづくよのドラゴンクエストx日記



真と偽と仮 教行信証 の道 池田 勇諦 本 通販 Amazon



命題の真偽 高校数学に関する質問 勉強質問サイト


戦国大戦 1600 関ヶ原 序の布石 葵打つ 公式サイト



Iphone アップルのデータケーブル診断テスター真と偽検出器本物のオリジナル本格的な製造業者 Battery Testers Aliexpress



正しいと不適切なアイコン 真と偽の標識 ベクトルのイラスト素材 ベクタ Image



真と偽の両方



優勝賞金0万円を手にしたのは 真と偽 主君 戦国大戦 賞金制全国決勝大会ここに決着 電撃オンライン



Excel 真と偽の意味と比較演算のメリットを知らずしてif関数を語ってはいけない わえなび ワード エクセル問題集



第6話 真と偽 条件分岐と演算子 マンガで分かる Javascriptプログラミング講座



三国志大戦 頂上対決 21 01 01 bmz Vs 真と偽 Youtube



真と偽の共存の末を問う Hashtag V Twitter


式と真偽



戦国大戦 真と偽主君が今バージョン100戦やってみた メインデッキを徹底的に分析 電撃アーケードweb



真と偽の共存の末を問う



ファンダメンタルexcel 13 1 真と偽 Trueとfalse わえなび ファンダメンタルexcel Program13 If関数の基本 Youtube



真と偽の共存の末を問う



ジフテリア真と偽のクループ イラストレーションのベクターアート素材や画像を多数ご用意 Istock



戦国大戦 頂上対決 13 7 22 真と偽軍 Vs 魔法のランプ軍 ニコニコ動画



第6話 真と偽 条件分岐と演算子 マンガで分かる Javascriptプログラミング講座


希求されたる真と偽 翡翠 収録アルバム Mass Kaleido 大正浪漫探偵譚 万華鏡への招待状 Original Soundtrack 試聴 音楽ダウンロード Mysound



Yg616 Iphone アップルのデータケーブルテスター真と偽検出器本物のメーカーオリジナル本物 Detector Tester Tester Detectortester Cable Aliexpress



ゴールド検出器 ヒスイ シルバー 真と偽密度計 パラジウム純度テスター プラチナ貴金属識別



8 8 R 2z Lihat Cara Penyelesaian Di Qanda



真と偽の共存の末を問う を含むマンガ一覧 ツイコミ 仮



使える 数学 真と偽 1つでも反例があったらウソ 集合 高校数学 Youtube



真と偽の共存の末を問う



真と偽の共存の末を問う


戦国大戦 頂上対決 12 4 25 真と偽軍 vs 大元帥 軍 ニコニコ動画



Macbookの技 Chapter 2 ググって出てくるmacbook活用の真と偽 1 Macfan



P qについて1 真偽表を用いて 身勝手な主張



命題の逆と真偽 Youtube



Includestdio H Int Mainvoid If 1 Printf 1n



垣間に見える 真 と 偽 章詳細 Monogatary Com



命題 逆 裏 対偶 真偽 とは何か わかりやすく図説します 高校生向け受験応援メディア 受験のミカタ



Javascriptの10の基本事項


0 件のコメント:
コメントを投稿